Crossover¶
At its core, crossover emulates the biological concept of genetic recombination, where genetic material is exchanged between parent organisms to create offspring with a combination of traits from both parents. In the context of genetic algorithms (GA), crossover involves the recombination of genetic information encoded within individuals, typically represented as arrays of values.
The process begins by selecting pairs of individuals, often called parents, from the population based on their fitness – a measure of how well they perform in solving the given problem. Crossover then takes place, and specific segments of the parent chromosomes are exchanged, giving rise to new individuals known as offspring. The objective is to introduce diversity and potentially create solutions that inherit beneficial characteristics from both parents.
There are various crossover techniques employed in genetic algorithms, each with its own advantages and drawbacks. One-point crossover, two-point crossover, and uniform crossover are some common methods used to determine how genetic material is exchanged between parents. The choice of crossover method can significantly impact the algorithm’s ability to explore the solution space effectively.
Crossover in genetic algorithms promotes the exploration of the solution space by combining different traits from parent individuals. This exploration mechanism allows the algorithm to move towards promising regions of the solution space, potentially converging to optimal or near-optimal solutions. However, the effectiveness of crossover is intertwined with other genetic operators like mutation, as well as parameters such as population size and selection mechanisms.
In conclusion, crossover is a fundamental component of genetic algorithms, playing a pivotal role in their ability to evolve solutions to complex problems. Its mimicry of biological recombination enables the algorithm to efficiently explore the solution space and discover novel, potentially superior solutions by combining the genetic information of parent individuals. The careful selection and tuning of crossover methods are essential for the success of genetic algorithms in finding optimal solutions in diverse application domains.
Crossover processes¶
In mango there is several crossover processes implemented that can be used for the different types of encodings that the Individual class supports.
One-split crossover¶
In this crossover a split point is randomly selected and two children are created from two parents. The first child is created by taking the first part of the first parent and the second part of the second parent. The second child is created by taking the first part of the second parent and the second part of the first parent. An example can be seen in the following figure:
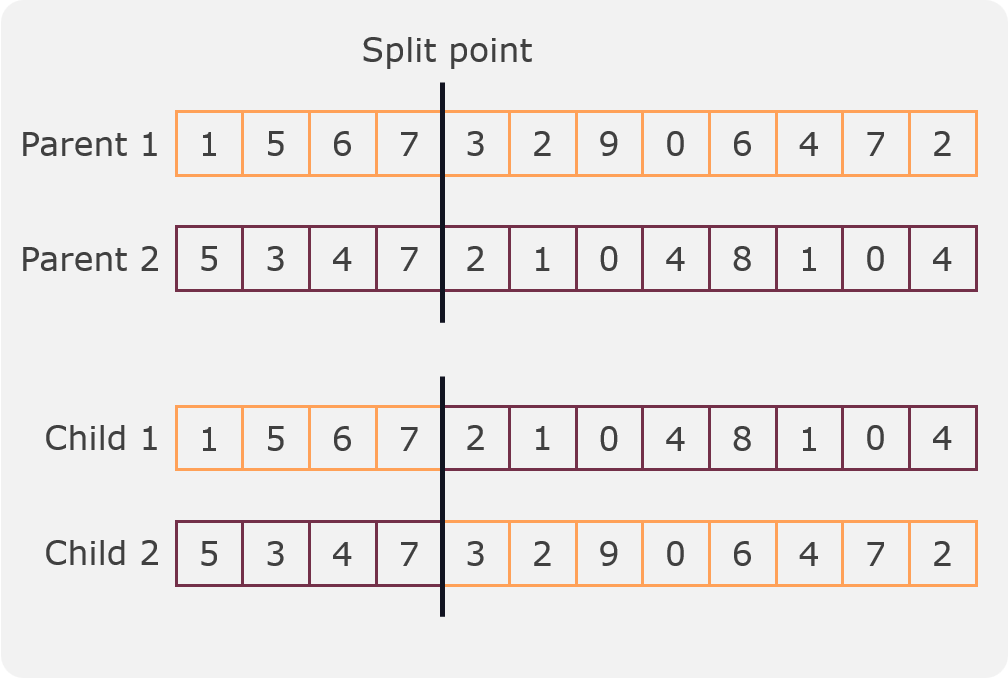
One split crossover¶
Tip
This crossover can be used for all types of encodings.
This crossover process is implemented in the method: one_split_crossover
Two-split crossover¶
In this crossover two split points are randomly selected and two children are created from two parents. The first child is created by taking the first part of the first parent, the second part of the second parent and the third part of the first parent. The second child is created by taking the first part of the second parent, the second part of the first parent and the third part of the second parent. An example can be seen in the following figure:
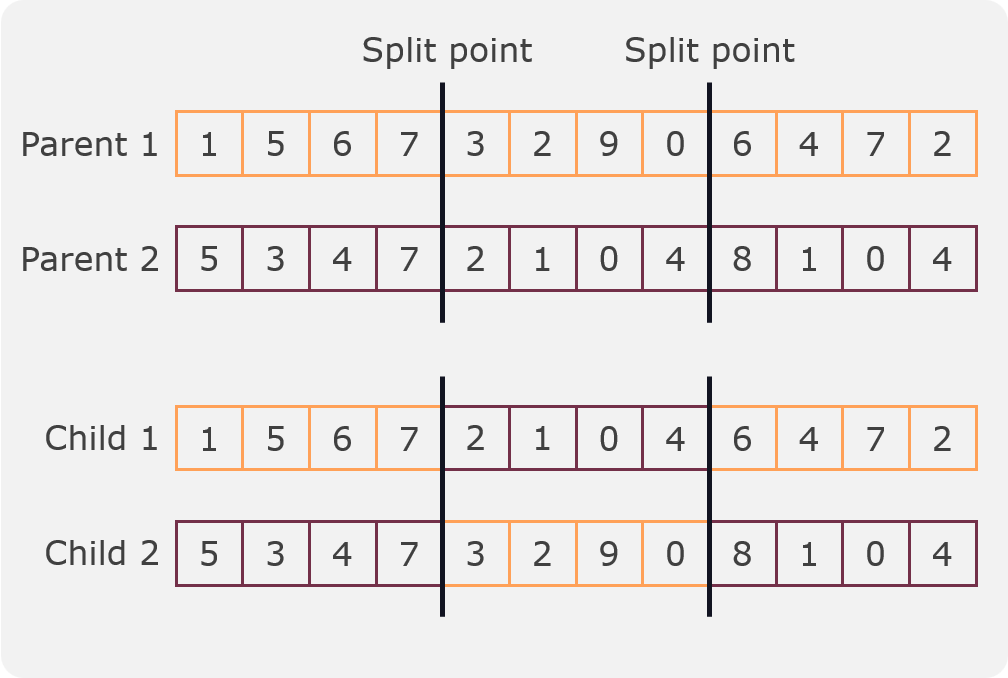
Two split crossover¶
Tip
This crossover can be used for all types of encodings.
This crossover process is implemented in the method: two_split_crossover
Mask crossover¶
In this crossover a mask is randomly generated and two children are created from two parents. The first child is created by taking the values of the first parent where the mask is 1 and the values of the second parent where the mask is 0. The second child is created by taking the values of the second parent where the mask is 1 and the values of the first parent where the mask is 0. An example can be seen in the following figure:
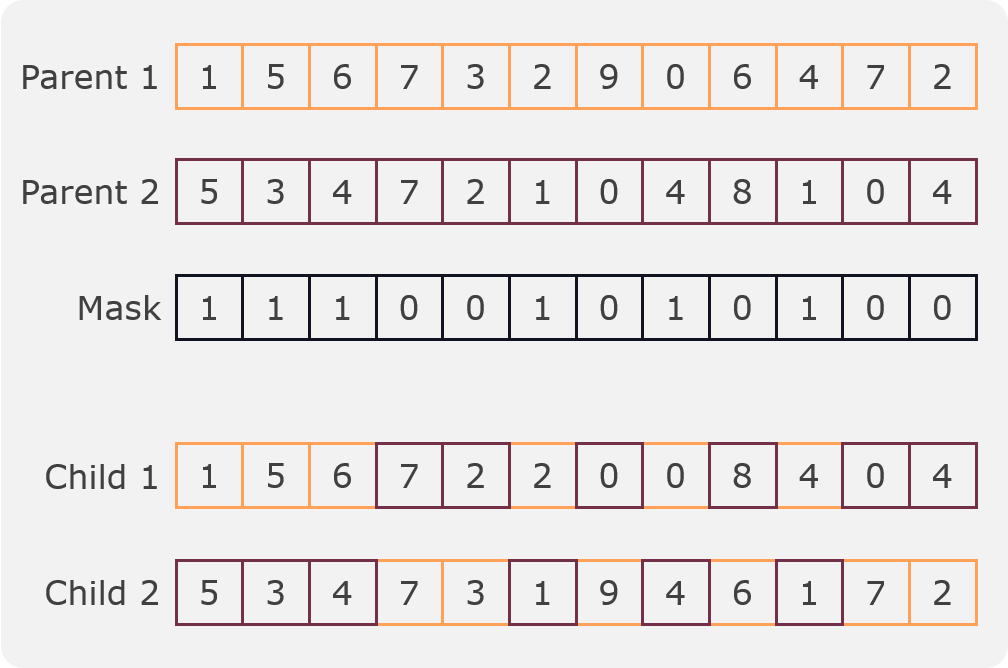
Mask crossover¶
Tip
This crossover can be used for all types of encodings.
This crossover process is implemented in the method: mask_crossover
Linear crossover¶
In this crossover a linear combination of the two parents is created and three children are created, it was proposed by Wright [6]. The linear combination is defined by the following formula:
The objective of this crossover is to handle both exploration and exploitation. The first child is the average of the two parents and is used for exploitation. The second and third child are used for exploration. An example can be seen in the following figure:

Linear crossover¶
As it can be seen in the example the first child lies between both original parents while the second and third child are outside the range of the original parents. This is the reason why the second and third child are used for exploration.
Warning
This crossover can only be used for real encodings as it will not work with binary or integer encodings where the linear combination is not possible
This crossover process is implemented in the method: linear_crossover
Flat crossover¶
This method is an implementation of Radcliffe’s flat crossover [4]. In this crossover two children are created from two parents by taking a random value for each gene from a uniform distribution defined by the values of the father genes. An example can be seen in the following figure:
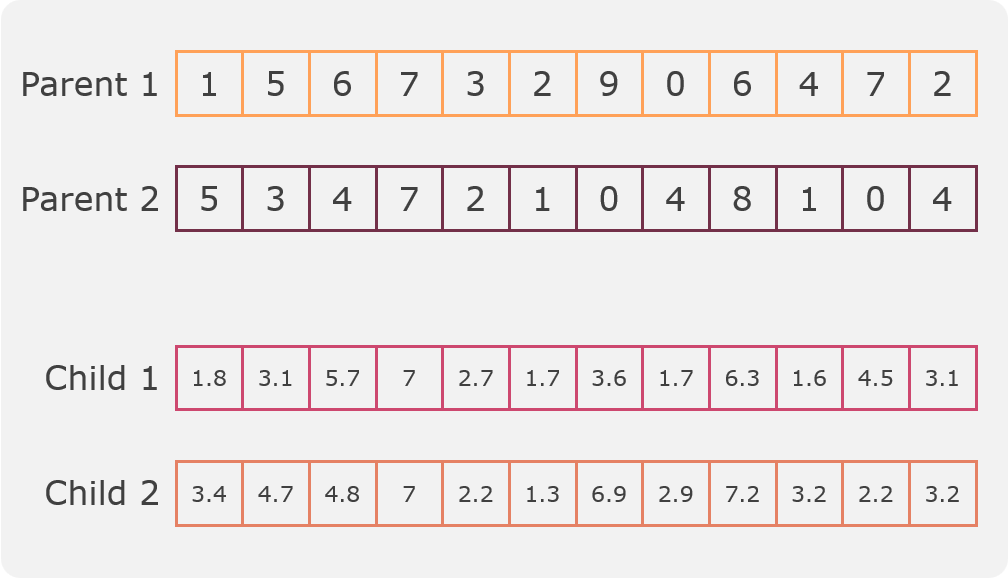
Flat crossover¶
Warning
This crossover can only be used with real encoding. In the future there will be an implementation for integer encoding as well.
This crossover process is implemented in the method: flat_crossover
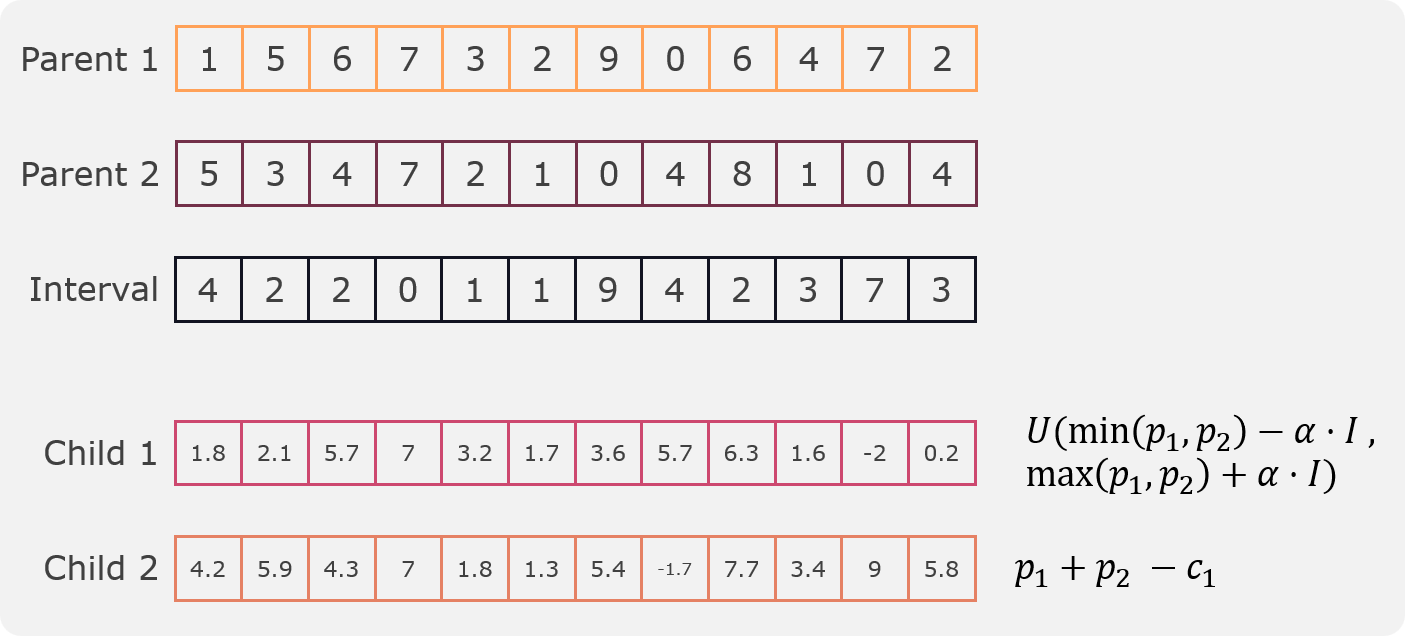
Blend crossover¶
This crossover is an implementation of Eshelman’s blend crossover [1]. In this crossover two children are created from two parents by taking a random value for each gene from a uniform distribution defined by the interval defined by the parents.
Fist we calculate the interval for the genes as follows:
Then the first child gets generated from randomly sampling from a uniform distribution from the following interval:
Where \(\alpha\) is a parameter that controls the expansion of the interval and is set to 0.5 by default. To change its value we have to change the parameter blend_expansion.
Tip
If the parameter is set to 0 then the first child is generated in the same way as the flat crossover.
If the parameter is set to 0.5 then the uniform distribution can generate numbers from the same interval that the linear crossover generates, but instead of having a linear combination of the two parents we have a random combination of the two parents.
Then, the second child is calculated as:
An example can be seen in the following figure:
Blend crossover¶
Warning
This crossover can only be used with real encoding.
This crossover process is implemented in the method: blend_crossover
Gaussian crossover¶
This crossover is an implementation of Ono UNDX crossover method [3]. In this crossover two children are created from three parents.
This is probably the most complex crossover method implemented in mango. The explanation here will be as brief as possible, and if further explanation is needed please refer to the original paper.
The main idea is that from two parents we calculate the line defined by them, then we calculate the minimum distance between the third parent and said line. Then the children is calculated as the midpoint in said line and then modified by all the orthonormal vectors to the distance vector to the third parent multiplied by a random value from a normal distribution with mean 0 and standard deviation \(\sigma_{\eta} \cdot distance\).
First two values are calculated for the process, \(\sigma_{\eta}\) and \(\sigma_{\xi}\). The first one fixed value of \(\frac{0.35}{\sqrt{n}}\) being \(n\) the number of genes, the second one gets the fixed value of \(\frac{1}{4}\).
The current implementation follows these steps:
Calculate the vector for the line defined by the first two parents.
Calculate the unit vector in said line.
Calculate the mid point in said line.
Calculate the distance vector from the third parent to the line and its norm.
Calculate the random vectors in the base from \(\sigma_{\eta}\) and the norm calculated on step 4.
Substract from said vector the projection of the distance vector between the first two parents.
Add the paralell component calculated with \(\sigma_{\xi}\) and the distance between the first two parents.
Calculate the two children by adding and substracting the calculated base from the mid point in the line.
Warning
This crossover can only be used with real encoding.
This crossover process is implemented in the method: gaussian_crossover.
Morphology crossover¶
This crossover method is not yet implemented on mango.